Soft Cache Simulation

• 1 - Simulator's parameters
  • 1.1 - Proxy-Client bandwidth
  • 1.2 - Proxy-Server bandwidth
  • 1.3 - Image Size
  • 1.4 - Reload Probability
  • 1.5 - Server Transmission Capability
  • 1.6 - Number of Images and Cache Size
  • 1.7 - Number of repetitions of the simulation
• 2 - Inside Simulator
• 3 - Results

Tables

• 1 - Input parameters
• 2 - Input parameters' values

Figures

• 1 - Distrubution of bc (Proxy-Client bandwidth)
• 2 - Distribution of bs (Proxy-Server bandwidth)
• 3 - Distribution of Ri (Image Size)
• 4 - Family of pr(ri/Ri) curves (reload probability given a part of image)
• 5 - Observed distribution of Ai
• 6 - Modelized Distribution of Ai
• 7 - Ai random generator
• 8 - Modelized Distribution of Ri
• 9 - Ri random generator
• 10 - Results of run #1, download time
• 11 - Results of run #2, download time
• 12 - Results of run #2, relative reduction in download time
• 13 - Results of run #2, relative cache usage

The simulator takes several parameters as input, and produces an output containing average download times for three scenarios: no cache at all, hard cache polocy, soft cache policy. Input parameters are described below and summarized in table 1.

From the study of acces.log files of our proxy server and from other available sources, has been obtained for proxy-client bandwidth the distribution shown in figure 1. Has been decided to modelize it as a gaussian curb, whose mean and variance are also shown in the figure.

As for proxy-client bandwidth, proxy-server bandwith's distribution has been obtained from access logs, the resulting curb and the gaussian chosen to modelize it are both shown in figure 2.

Image size distribution is the third and last parameter whose distribution is extracted from access logs (there is also a built-in variable discussed later in par. 2.1). In figure 3 are shown the actual distribution and the gaussian that better approximates it.

The users' bahaviour is modelized by a curb chosen in the family of (1-(ri/Ri))^m, figure 4 shows curves for some choice of m.

Number of images I and cache size CS could be treated toghether, figure 10 shows that for a number of images sufficiently big, varying these quantities proportionally lead to analogous results.

<-- Back to Table of Contents

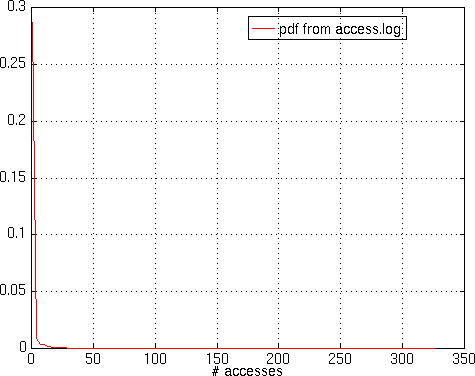
This is a built-in random variable, whose model has been chosen by studying access logs during a fixed period (24 hours). Figure 5 shows, or doesn't show, the distribution of this variable, figure 6 shows the model that has been chosen, a negative exponential.

In the simulation there are two types of random variables: negative exponential for Ai, and gaussian for bandwidths and image size.
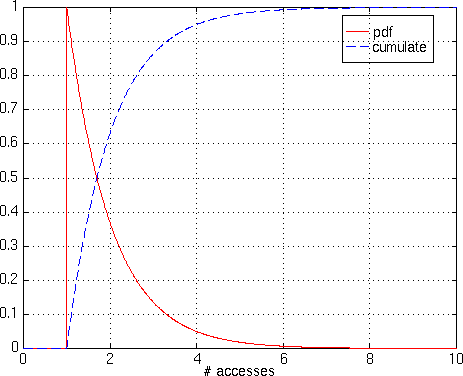
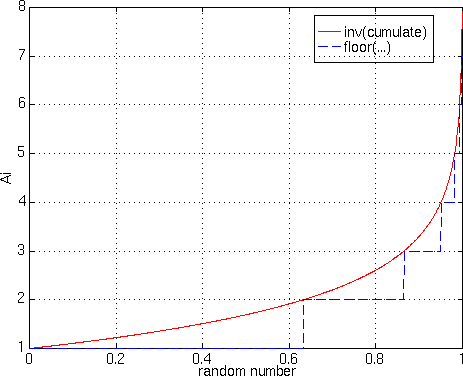
Figure 6 shows the distribution of Ai and the cumulative function, figure 7 shows the inverse cumulative function, used for generating the exponential random variable from a linear random variable.
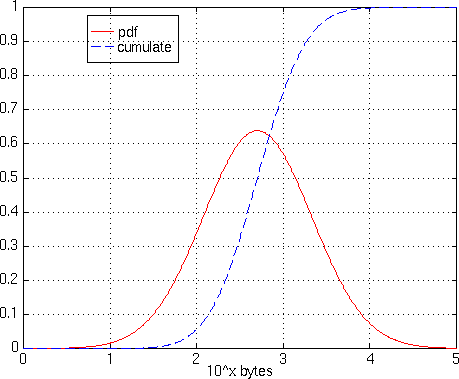
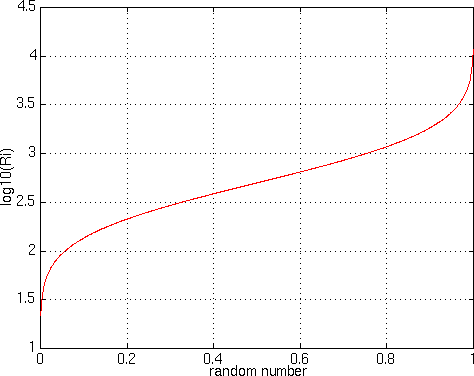
Figure 8 reports the modelized distribution of Ri (as an example of gaussian distribution), figure 9 shows the inverse cumulate probablity function, theoretically used for generating gaussian random variables from linear random variables. In the actual implementation of the simulator a more efficient algorithm is used.

<-- Back to Table of Contents

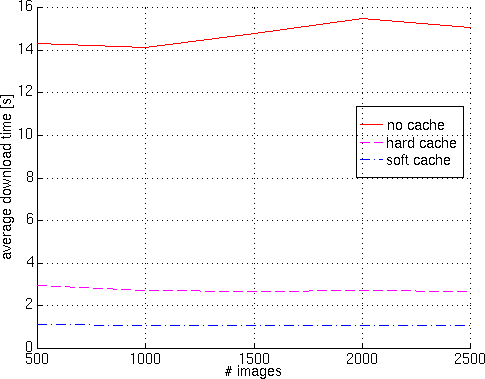
In table 2 there are the input parameters' values for two runs of the simulator.
The first run aims to show that if the ratio between number of images and cache size is constant, results are not dependent on these two parameters, thus the number of images can be kept small in order to make faster simulations.
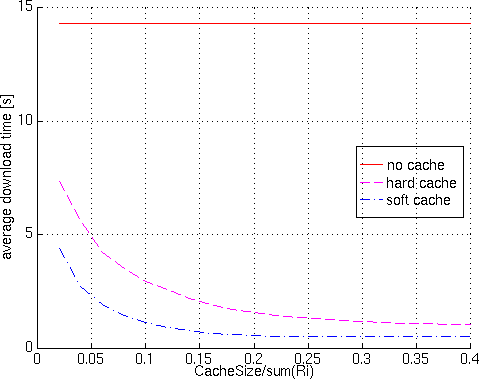
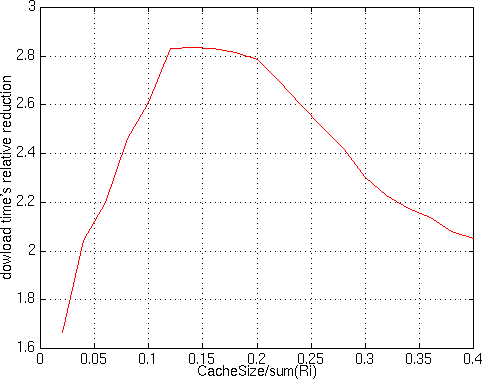
Run #2 tests the cache whith different load sizes, it starts with cache size as big as 2% of total images size, and goes to cache size equal to 40% of total images size. Results of run #2 are shown in figure 11 through figure 13. It can be seen that download time (figure 11) keep decreasing as the cache becomes bigger, both for soft and hard caching policies, but figure 12 shows that the relative gain of soft cache w.r.t. hard cache has a maximum at about 15% (cache size = 15% of total images size). 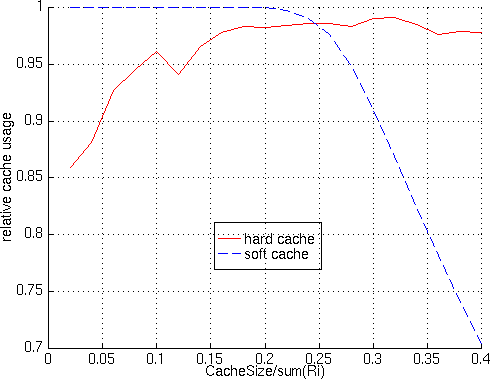In addition, it can be seen from figure 13 that the algorithm implemented finds an optimal cache usage for soft cache policy until cache size reachs 20%, then cache usage for soft cache drops and at about 25% hard cache becomes the better policy in terms of cache usage.

<-- Back to Table of Contents