The basic difference between the Lagrangian and dynamic programming (DP) approaches is that the Lagrangian approach is limited to select only operating points on the convex hull of the overall R-D characteristic. No such constraint affects the DP approach.
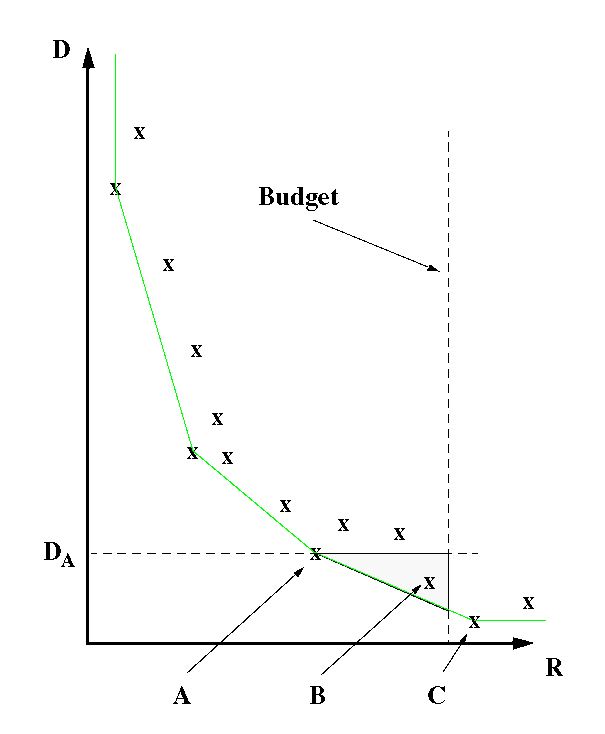
This can be easily seen with the example of the figure below, which represents the combined R-D characteristic for a set of coding units. The figure shows an instance of the problem of Formulation where rate has to be allocated to coding units in order to meet a budget constraint. In Fig. the operating point C exceeds the budget and thus is not an admissible solution. The nearest convex hull point (A) has higher distortion than B. Therefore B would be the optimal solution for the problem at hand. In fact, any points in the shaded are would be better than A. However, none of them is reachable using Lagrangian techniques, as these points are located ``over'' the convex hull. However these points would be reachable through dynamic programming.
Note that this situation comes about because we are dealing with a discrete allocation and therefore the set of achievable points on the convex hull is also discrete (the example of Box F assumes a continuous range of choices and thus the Lagrangian approach is indeed optimal in that case.) In many instances, in particular when the convex hull is densely populated, this situation is less likely to arise or in any case the gap between the best Lagrangian solution and the optimal solution may be small. Exceptions include scenarios where the number of coding units is small and the convex hull is sparse, as for example in the coding for Scalar Vector Quantization (SVQ) . When that is the case, the performance gap may be larger and using DP all the more important. However it may also be possible to use a Lagrangian solution to initialize the DP search .
In terms of complexity, the Lagrangian approach is preferable, since it can be run independently in each coding unit, whereas DP requires a tree to be grown. The complexity of the DP approaches can grow exponentially with the number of coding units considered while the Lagrangian approach's complexity will only grow linearly. Thus in many situations the Lagrangian approach is a sufficiently good approximation once computation complexity has been taken into account.
